12/17　G検定

Chain-of-Thoughtチェーンオブソート　

Chain-of-Thoughtプロンプティングは、対話型AI（例：ChatGPT）を効果的に活用するためのプロンプト作成技術です。この手法では、入力に思考の過程を明示的に示すことで、より望ましい出力を引き出すことができます。

主なポイント

• 略称: Chain-of-Thoughtは「CoT」と略されることがあります。
• 思考過程の提供: ユーザーが思考の過程を入力として与えることで、AIの出力が改善されます。
• 自己思考: AI自身に考えさせることでも、出力の質が向上する場合があります。これもChain-of-Thoughtと呼ばれることがあります。

この技術を用いることで、AIとの対話がよりスムーズで効果的になるでしょう。

IBM：https://www.ibm.com/jp-ja/topics/few-shot-learning

思考過程を入力しておくと数学の文章問題や推論の正答率が上がる

Transformer　

transformerは長い文章を翻訳しようとすると最初の方は訳してくれなかったが
transformerで解決する
attentionという機構のみでネットワークを構築

RNNの問題を克服したmodel

畳み込みニューラルネットワーク（CNN）
リカレントニューラルネットワーク（RNN）並列処理ができなかった

参考：https://data-science.media/ai-information/deep-learning-application-example/

データアクセス

オブジェクトストレージとはなんですか？オブジェクトストレージの記述として，最も適切なものはどれか。

もちろん、雰囲気を変えて説明しますね。

オブジェクトストレージの概要

オブジェクトストレージは、従来の階層型ファイルシステムとは異なり、データを「オブジェクト」として管理します。これにより、フラットな構造でスケールアウトが容易になり、特に非構造型データを大量に扱うデータレイクに最適です。代表的なサービスとしては、Amazon S3があります。

特徴

• 各オブジェクトには、データ本体、メタデータ、固有の識別子が付与されます。
• 階層構造がないため、以下の利点があります：

1. データの複製や移動が簡単
2. 効率的なアクセスが可能
3. ディレクトリ数やデータ数の制限がない

アクセス方法

オブジェクトストレージは、REST API（HTTP）を介してアクセスします。これにより、ユーザーはデータの格納場所を覚える必要がなく、さまざまなプラットフォームから一貫した手順で操作ができます。

その他のストレージタイプ

• SAN (Storage Area Network):
  高速のストレージ専用ネットワークを利用して、複数のサーバからストレージを共有し、高速にデータを格納します。
• DAS (Direct Attached Storage):
  各サーバに専用のストレージを割り当て、容量が不足した場合には簡単に追加できます。
• RAID (Redundant Arrays of Inexpensive Disks):
  複数のストレージを組み合わせることで、仮想的に1台のストレージとして運用可能です。

このように、オブジェクトストレージは特に大容量で拡張性のあるストレージを必要とするシナリオにおいて、非常に有効な選択肢となります。

zero-shotは既存のモデル

参考：https://ai-market.jp/howto/zero-shot-learning/

参考：https://zero2one.jp/ai-word/zero-shot/?srsltid=AfmBOooS-oyfPsw2XUzmMpGR0uv2BbC91RfuiZH1Oikz_h6eYlka34hc

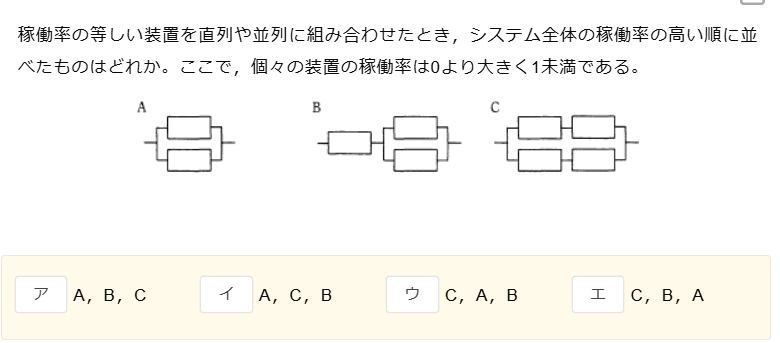
稼働率が等しい装置Xを直列や並列に組み合わせた時

もちろん、雰囲気を変えて説明しますね。

システムの稼働率の比較

各装置の稼働率が等しく、0より大きく1未満であると仮定し、ここでは稼働率を0.9と設定します。この条件のもと、システム全体の稼働率を比較してみましょう。

システムA

2台の装置が並列接続されています。

• 稼働率の計算式：
  [
  R_A = 1 – (1 – 0.9)^2 = 1 – 0.12 = 1 – 0.01 = 0.99
  ]

システムB

システムAに装置1台が直列接続されています。

• 稼働率の計算：
  [
  R_B = 0.9 \times R_A = 0.9 \times 0.99 = 0.891
  ]

システムC

装置2台が直列接続され、その結果が並列接続されています。

• 稼働率の計算：
  [
  R_C = 1 – (1 – 0.9)^2 = 1 – (1 – 0.81)^2 = 1 – 0.192 = 1 – 0.0361 = 0.9639
  ]

結果のまとめ

したがって、稼働率の高い順にシステムを並べると、次のようになります：

• A > C > B

別解による論理的なアプローチ

各システムの稼働率を一般化して式で表し、比較してみます。装置の稼働率をRとします。

• Aの稼働率:
  [
  R_A = 1 – (1 – R)^2
  ]
• Bの稼働率:
  [
  R_B = R \times R_A = R \times (1 – (1 – R)^2)
  ]
• Cの稼働率:
  [
  R_C = 1 – (1 – R^2)^2
  ]

稼働率の大小比較

• AとB:
  [
  a > Ra \quad \Rightarrow \quad A > B
  ]
• AとC:
  [
  (1 – R) < (1 – R^2) \quad \Rightarrow \quad A > C
  ]
• BとC:
  Bの稼働率を展開すると、
  [
  R(2R – R^2) = R^2(2 – R)
  ] Cの稼働率を展開すると、
  [
  2R^2 – R^4 = R^2(2 – R^2)
  ]

この比較から、次のように結論づけられます：

• B < C

結論

最終的に、3つのシステムの稼働率を高い順に並べると、次のようになります：

• A, C, B

Validia